БіржаDEX+

Купити криптовалюту Ринки Спот Ф'ючерси500X Earn Події

Ще

Розіграш золотого злитка та BTC2000g

Фрактали — це нескінченні візерунки, створені повторюваними математичними рівняннями. Ми намалюємо один із найвідоміших фракталів, використовуючи лише Vanilla JS та HTML5 Canvas API.Фрактали — це нескінченні візерунки, створені повторюваними математичними рівняннями. Ми намалюємо один із найвідоміших фракталів, використовуючи лише Vanilla JS та HTML5 Canvas API.

Кодування фрактального дерева за допомогою JavaScript та HTML5

Автор: Hackernoon

2025/10/11 03:00

Поділитись

TREE$0.1197+1.52%

LL$0.007914+0.12%

\ Фрактали, ті загадкові фігури, які є всюди, але не можуть бути побачені непідготовленим оком. Сьогодні ми намалюємо один із найвідоміших фракталів, використовуючи лише Vanilla JS та HTML5 Canvas API. Давайте кодити!

Що ви вивчите

Що таке фрактальне дерево?
Написання фрактального дерева на Vanilla JS
За межами фрактального дерева

Що таке фрактальне дерево?

Щоб визначити фрактальне дерево, спочатку ми повинні знати визначення фракталу, звичайно.

Фрактали - це нескінченні візерунки, створені повторенням математичних рівнянь, які на будь-якому масштабі, на будь-якому рівні збільшення, виглядають приблизно однаково. Іншими словами, геометричний об'єкт, основна структура якого, груба чи фрагментована, повторюється в різних масштабах.

Отже, якщо ми розділимо фрактал, ми побачимо зменшену копію цілого.

Бенуа Мандельброт, який придумав термін "фрактал" у 1975 році, сказав:

\ Досить зрозуміло, правда?

Ось кілька прикладів:

Animated Von Koch Curve

\ Animated Sierpinski Carpet

Тепер, що таке фрактальне дерево?

Уявіть гілку, і гілки, що виходять з неї, а потім дві гілки, що виходять з кожної гілки, і так далі... ось як виглядає фрактальне дерево.

Його форма походить від трикутника Серпінського (або килима Серпінського).

Як бачите, одне стає іншим при зміні кута між гілками:

From Sierpinski Triangle to Fractal

Сьогодні ми закінчимо з фігурою, подібною до кінцевої форми цього GIF.

Написання фрактального дерева на Vanilla JS

Перш за все, ось кінцевий продукт (ви можете налаштувати його по ходу):

Final Fractal Tree

Тепер давайте намалюємо це крок за кроком.

Перш за все, ми ініціалізуємо наш файл index.html з полотном будь-яких розумних розмірів і тегом script, де буде весь наш JS-код.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script></script>   </body> </html>

Потім ми починаємо писати наш JavaScript.

Ми ініціалізуємо наш елемент canvas в JS, отримуючи до нього доступ через змінну myCanvas і створюючи 2D-контекст рендерингу за допомогою змінної ctx (контекст).

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");     </script>   </body> </html>

Отже, метод getContext додає властивості та методи, які дозволяють вам малювати, в даному випадку, в 2D.

Тепер час подумати. Як ми можемо визначити алгоритм для малювання фрактального дерева? Хм... 🤔

Давайте подивимося, ми знаємо, що гілки продовжують ставати меншими. І що кожна гілка закінчується двома гілками, що виходять з неї, одна ліворуч, а інша праворуч.

Іншими словами, коли гілка достатньо довга, приєднайте до неї дві менші гілки. Повторно.

Це звучить так, ніби ми повинні використовувати десь рекурсивний оператор, чи не так?

Повертаючись до коду, тепер ми визначаємо нашу функцію fractalTree, яка повинна приймати принаймні чотири аргументи: координати X і Y, де починається гілка, довжину її гілки та її кут.

Всередині нашої функції ми починаємо малювання з методу beginPath(), а потім зберігаємо стан полотна за допомогою методу save().

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();       }     </script>   </body> </html>

Метод beginPath часто використовується, коли ви починаєте нову лінію або фігуру, яка має фіксований стиль, наприклад, однаковий колір вздовж всієї лінії або однакову ширину. Метод save просто зберігає весь стан полотна, поміщаючи поточний стан у стек.

Тепер ми намалюємо наше фрактальне дерево, малюючи лінію (гілку), обертаючи полотно, малюючи наступну гілку і так далі. Це виглядає так (я поясню кожен метод під зразком коду):

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle) {           ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, -15);           draw(0, -len, len*0.8, +15);            ctx.restore();       }       draw(400, 600, 120, 0)     </script>   </body> </html>

Отже, спочатку ми додаємо три методи: translate, rotate і moveTo, які "переміщують" полотно, його початок і наш "олівець", щоб ми могли намалювати гілку під потрібним кутом. Це ніби ми малюємо гілку, потім центруємо цю гілку (переміщуючи все полотно), а потім малюємо нову гілку з кінця нашої попередньої гілки.

Останні два методи перед оператором if - це lineTo і stroke; перший додає пряму лінію до поточного шляху, а другий її відображає. Ви можете думати про це так: lineTo дає наказ, а stroke його виконує.

Тепер у нас є оператор if, який вказує, коли зупинити рекурсію, коли припинити малювання. Метод restore, як зазначено в документації MDN, "відновлює найбільш недавно збережений стан полотна, виштовхуючи верхній запис у стеку стану малювання".

Після оператора if у нас є рекурсивний виклик і ще один виклик методу restore. А потім виклик функції, яку ми щойно закінчили.

Тепер запустіть код у своєму браузері. Ви побачите, нарешті, фрактальне дерево!

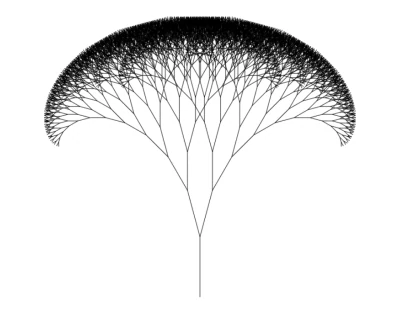
Fractal Tree First Iteration

Чудово, правда? Тепер давайте зробимо його ще кращим.

Ми додамо новий параметр до нашої функції draw, branchWidth, щоб зробити наше фрактальне дерево більш реалістичним.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Отже, в кожній ітерації ми робимо кожну гілку тоншою. Я також змінив параметр кута в рекурсивному виклику, щоб зробити більш "відкрите" дерево.

Тепер давайте додамо трохи кольору! І тіні, чому б і ні.

<!doctype html> <html lang="en">   <head>     <meta charset="UTF-8" />   </head>   <body>     <canvas id="my_canvas" width="1000" height="800"></canvas>     <script>       var myCanvas = document.getElementById("my_canvas");       var ctx = myCanvas.getContext("2d");       function draw(startX, startY, len, angle, branchWidth) {           ctx.lineWidth = branchWidth;            ctx.beginPath();           ctx.save();            ctx.strokeStyle = "green";           ctx.fillStyle = "green";            ctx.translate(startX, startY);           ctx.rotate(angle * Math.PI/180);           ctx.moveTo(0, 0);           ctx.lineTo(0, -len);           ctx.stroke();            ctx.shadowBlur = 15;           ctx.shadowColor = "rgba(0,0,0,0.8)";            if(len < 10) {               ctx.restore();               return;           }            draw(0, -len, len*0.8, angle-15, branchWidth*0.8);           draw(0, -len, len*0.8, angle+15, branchWidth*0.8);            ctx.restore();       }       draw(400, 600, 120, 0, 10)     </script>   </body> </html>

Обидва методи кольору є самопояснювальними (strokeStyle і fillStyle). Також і методи тіні, shadowBlur і shadowColor.

І це

Відмова від відповідальності: статті, опубліковані на цьому сайті, взяті з відкритих джерел і надаються виключно для інформаційних цілей. Вони не обов'язково відображають погляди MEXC. Всі права залишаються за авторами оригінальних статей. Якщо ви вважаєте, що будь-який контент порушує права третіх осіб, будь ласка, зверніться за адресою [email protected] для його видалення. MEXC не дає жодних гарантій щодо точності, повноти або своєчасності вмісту і не несе відповідальності за будь-які дії, вчинені на основі наданої інформації. Вміст не є фінансовою, юридичною або іншою професійною порадою і не повинен розглядатися як рекомендація або схвалення з боку MEXC.